Massimo Capone: Signatures of strongly corelated superconductivity in expanded fulleride Cs3C60

Massimio gives us the outline: pairing in the alkali doped fullerides is most likely phonons but with pecularities which grows with lattice spacing. There is a Mott transition close to the first order superconducting transition.
We stand now with apparently two distinct classes of superconductivity:

• Low Tc: phonon mediated, normal metal above Tc
• High Tc: electronic mechanism and a strange metallic state

But are these two distinct divisions. After all the heavy fermions are presumably electronic but with low Tc (my comment: of course all the energy scales are low there). Claim that the fullerides may show aspects of both. So where do the alkali metal doped fullerides belong?

Start with the parent: C60 - a molecular crystal, a band insulator with three fold degenerate LUMO.

Now doped: AnC60: the alkali donate their s-electrons. Highest Tc is with n=3. But why a superconductor. At first sight these are ordinary BCS superconductors. There is a carbon isotope effect, a regular specific heat jump and Tc increases with density of states as the lattice spacing is changed. Piers asks for clarification about the relation between lattice spacing and the density of states: naively the increasing in spacing lowers the wavefunction overlap and so increases the density of states - is that right? Yes: but perhaps the correlations are effected too - a key point for the talk.
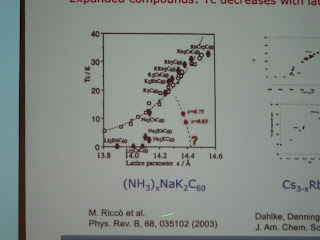
However some interesting features emerge on expanding the lattice with NH3, or mixing Cs and Rb as the metals. In both cases the DOS (from Knight shift) increases but Tc goes down. Moreover some related compounds become Mott insulators - suggestive of enhanced correlations. K4C60 is a spin-gapped insulator.

Now enter the A15 structured (bcc) Cs3C60 which is non-superconducting at ambient pressure and yet has very large lattice spacing. It superconducts from 4-7 kbar with Tc(max)=38K reminiscent of the phase diagram of the cuprates and further pressure gets you to an AFM phase with TN=40K S=1/2. There seems to be some coexistence of superconductivity and AFM. Andrey asks about the coexistence region. Henri answers: this is a materials issue and that a pure system has a first order transition with no coexistence. Contrasting with the fcc structure Cs3C60 has exactly the same Tc dome as a function of pressure but the scale of the AFM is an order of magnitude lower. Thus magnetism is not setting the scale of the superconductivity. Massimo claims that Mott is the key to superconductivity - but Piers plays devils advocate and says its separated from the metal by a first order transition so why should it have anything to do with the superconductivity? Claim that the talk will answer this...
Now to theory (which predates these recent experiments...) . A three band Hubbard model (with band width of order 0.5eV and U ~ 1 or 1.5eV) so correlations playing a role. The add a Hund's rule:
-JH(2S^2_i + (1./2)L_i^2) - (5/6)J_H(n_i-3)^2
and then add electron-phonon: a t_{1u} electrons coupled to the H_+{1g} which contains some Jahn-Teller physics.
The claim is that this coupling mirrors the Hund's rule coupling but with an opposite sign - they play a negative role. Unlike the usual case where slow phonons overscreen the local Coulomb interaction, here retardation plays less of a role since it fights with the Hund's rule rather than Coulomb. Taking realistic numbers the e-ph coupling exceeds the Hund's rule so the phonons favour a small S state inverting the usual Hund's rule.
Now we try and extract some physics first from the small U/W limit: Perturbation theory gives an s-wave superconductivity - adding U then there is a competition and if U> J_eff there is no superconductivity.
Now think of U>>W. Three electrons become stuck on the site (bucky ball) but J is free to act and so it forms a low spin S=1/2 state (consistent with later expeiments). But still no superconductivity. So to look for superconductivity Massimo and colleagues to DMFT. Its a good first step since the interactions are all assumed to be local to the Buckyballs. Now we are being reminded of the DMFT approach to the Mott transition showing the upper and lower Hubbard bands and a quasiparticle band in between which has Z->0 and m^* diverging. The solution (on a bipartite Bethe lattice) of the DMFT equations gives a phase diagram with metal, s-wave superconductor and then AFM as U/W is increased (ie like increased pressure). The plot seems to show coexistence of AFM and superconductivity and Ken questions it. Massimo clarifies that two solutions exist at that point but it does not mean they coexist. Erio says it is a bad figure.
Question: Andriy asks how come s-wave exists in a large U limit? Erio answers that this is a multi-orbital system which allows the electrons to avoid each other while still pairing in the s-wave channel. In more detail: they find that U is effectively renormalized downwards with the quasiparticle Z as the Mott transition approaches for the quasiparticle, but J is unrenormalized and so eventually wins to and drives superconductivity. But how come J is unrenormalized. Mott freezes out the charge fluctuations but the spin and orbital degrees if freedom are still fluctuating: J_eff ~ Z^2 L_s^2 J ie the vertex correction cancels the Z since L+s ~1/Z. YuLu asks is there a Ward identity protecting it? Piers asks what symmetry is there left which is conserved and would spin-orbit coupling prevent this? An open question...
Now into the final part of the talk and Massimo introduces a simple model with just two bands and an inverted J which they can also treat in DMFT. Some insight comes from the impurity model which has a critical point sick with groundstate entropy. On the lattice superconductivity quenches this and sharpens the quasiparticle peak and gives a contribution to the condensation energy (like, it is claimed, in the underdoped cuprates). So a prediction is that the superfluid contribution to the optical conductivity is larger than the Drude weight of the metal. They also compute the specific heat jump, uniform susceptibility and photo-emission spectra (with a pseudogap). So the normal state should not be so normal and there are testable predictions.
See Rev Mod Phys 81, 943 (2009).

Question time:
Andrei C.: Is Z a constant or should it really be frequency dependent - do you see this? Answer the complexity of the three-band model means Massimo can not reliably be confident in any statements about this, but he does not think it is relevant.
Henri: What is the pseudogap in this model? Answer: it is J in the model and is more or less constant with U/W. Henri so would you not expect it to go to zero in the metallic side? Yes
Zlatko: This is really just an electron-phonon superconductor? Answer: yes.
Piers: what about the spin entropy - how much goes into the condensation energy? If it is a lot, as 3/2 to 1/2 to 0 suggests, then this should be very different from an electron-phonon superconductor. Answer: I think it is log(2). Piers - so this is massively different from an electron-phonon superconductor so the answer to Zlatko's question should be no!
Q: (Sorry I missed this in typing the above...)